| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- BOJ
- 해설
- BFS
- Recursive
- 영화
- 완전탐색
- 카카오
- 넷플릭스
- health
- silver
- coding
- review
- 백준
- Movie
- array
- 2020
- 알고리즘
- usaco
- kakao
- 나는솔로
- 영어
- 수능
- Netflix
- parametric search
- Greedy
- Algorithm
- 추천
- benefits
- 코딩 테스트
- 리뷰
- Today
- Total
Young
그래프를 프로그래밍으로 어떻게 표현하는가 본문
어려운 코딩 테스트에서는 그래프 문제가 하나씩 출제 됩니다.
코딩 테스트 그래프 관련 문제라고 한다면, 아래 수준에서 나옵니다.
1. 최단거리 (플로이드 알고리즘 / 다익스트라 알고리즘)
2. 트리
3. 싸이클 찾기
4. 최소 스패닝 트리
이러한 문제를 푸는데 가장 먼저 해야할 것은 '노드와 노드를 엣지로 잇는 것' 입니다.
이것을 구현하는 방법에는 크게 두 가지가 존재합니다.
1. adjacent matrix
2. adjacent list
이 두 가지에 대해서 살펴볼 예정입니다.
그 전에 일반적으로 그래프의 두 가지 종류에 대해서 말씀드리겠습니다.
1. directed graph (방향 그래프) : 문제에서 주어진 그림에 화살표가 있거나, 문제 설명에 'a에서 b로만 갈 수 있다'라는 말이 있을 경우
2. undirected graph (무방향 그래프) : 문제 주어진 그림에 화살표가 없거나, 양방향 이동이 가능하다고 설명되어 있는 경우
위 두 그래프는 특별히 다룰 필요는 없습니다. 다만, 정의가 저렇다는 정도는 알고 있으면 됩니다.
이제는 그래프 디자인을 해봅시다.
1. adjacent matrix

이 방법의 장/단점에 대해서 알아보겠습니다.
<장점>
1. 직관적인 디자인으로 쉽게 알아볼 수 있다.
2. 짧은 코드로, 노드 a에서 노드 b로 갈 수 있는지를 빠르게 확인할 수 있다.
<단점>
1. 노드의 수가 많아질 경우, 메모리를 많이 차지하게 된다. 노드의 수가 10,000개만 되어도 만들기 힘들다.
2. 1번과 비슷한 말이다. 노드 수는 많지만, 엣지 수는 매우 적은 경우 메모리가 낭비된다.
위와 같은 사항들을 숙지하고, 상황에 맞게 사용해 주면 됩니다.
이제 코드로 어떻게 이를 적용하는지 봅시다.
https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 100)이 주어지고 둘째 줄에는 버스의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다. 시작
www.acmicpc.net
아래 코드는 위 문제에 대한 코드입니다.
아래 코드에서 이 그래프를 만드는 부분은 8~18 번째 줄까지 부분 입니다.
8~10 : 배열에 문제에서 나올 수 없는 최댓값으로 초기화함으로써 모든 노드 사이를 끊는 작업을 한다. 즉, 엣지가 없게 한다.
13~18 : 이 문제의 경우 directed graph가 아니기 때문에 17줄을 주석처리 했지만, undirected 일 경우 17줄 또한 실행해주어야 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
const int INF = 1000000000; // 나올 수 없는 경로의 길이 값
int main() {
int n, m, dist[101][101];
cin >> n >> m;
// dist 배열 초기화
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
dist[i][j] = i == j ? 0 : INF;
// 간선 정보 입력받음
for (int i = 0; i < M; i++) {
int a, b, c;
cin >> a >> b >> c;
dist[a - 1][b - 1] = min(dist[a - 1][b - 1], c);
//dist[b - 1][a - 1] = min(dist[b - 1][a - 1], c);
}
// 플로이드 와샬 알고리즘 적용
for (int k = 0; k < N; k++)
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
// 이제 dist 배열은 실제 최단 경로를 담고 있음
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cout << dist[i][j] == INF ? 0 : dist[i][j] << endl;
}
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
2. adjacent list
이 방법의 장/단점에 대해서 알아봅시다.
<장점>
1. 엣지가 연결되어 있지 않은 경우, 불필요한 메모리를 사용할 필요가 없다.
<단점>
1. 만약 a노드에서 b노드로 갈 수 있는지 판단할 때 코드가 좀 더 복잡해지고, 시간도 더 오래걸린다.
2. 같은 간선 정보가 또다시 들어오게 되면, 이를 처리하기 위한 로직을 만들시 시간 복잡도가 너무 커진다.
만약 처리 로직을 만들지 않을 때 오히려 메모리가 터지는 테스트 케이스가 있을 수도 있다.
그래서 보통 문제에서는 엣지 정보를 한 번 씩만 준다던지, 엣지 정보가 적다던지 합니다.
3.
https://www.acmicpc.net/problem/17825
17825번: 주사위 윷놀이
주사위 윷놀이는 다음과 같은 게임판에서 하는 게임이다. 가장 처음에는 시작에 말 4개가 있다. 말은 게임판에 적힌 화살표의 방향대로만 이동할 수 있다. 파란색 칸에서 말이 이동을 시작하는 경우에는 파란색 화살표의 방향으로 이동해야 하며 파란색 칸을 지나가는 경우에는 빨간 화살표의 방향대로 이동해야 한다. 게임은 1부터 5까지 한 면에 하나씩 적혀있는 5면 주사위를 굴려서 나온 수만큼 이동하는 방식으로 진행한다. 이동하려고 하는 칸에 말이 이미 있는 경우에
www.acmicpc.net
위 문제를 통해 연습해보겠습니다.
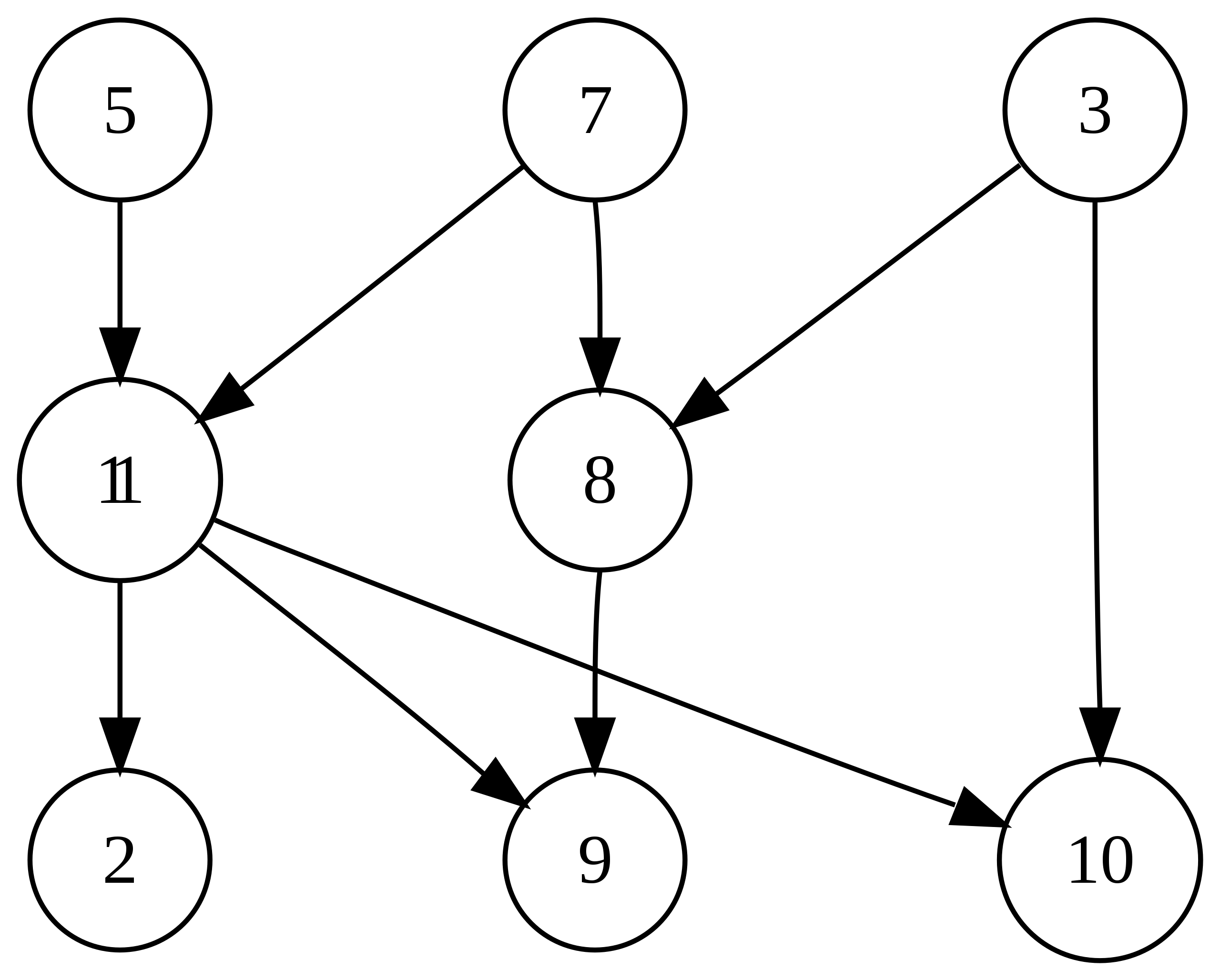
우선 아래와 같이 노드에 번호를 붙였습니다.
문제에서 엣지를 귀찮아서 그리지 않았지만 분명히 방향이 있는 그래프 입니다.
이 노드들 사이를 엣지로 연결해야 하는데 이를 어떻게 하나 봅시다!

c++ 에서는 이를 구현하기 위해 vector 배열을 사용합니다.
만약, 노드 갯수가 최대 10000개 들어올 수 있다면, 맨 처음에 vector<int> v[10000]; 이렇게
선언을 해주고 시작합니다.
간선 정보 a, b (노드 a에서 노드 b로 갈 수 있는 간선)가 주어지면, v[a].push_back(b); 이렇게 넣어줍니다.
이렇게 되면, v[a] 백터 안에는 노드 a에서 갈 수 있는 모든 간선의 정보를 담고 있습니다.
그래프를 모두 순회하기 위해서 각 노드에서 갈 수 있는 간선들을 모두 조사해보아야 하는데,
보통 for(int next : v[a]) { ... } 이런 식으로 조사를 해봅니다.
v[i][0] 은 그 다음 노드의 번호를 담고 있습니다.
이런식으로 연결을 해주는 겁니다!
파란색 화살표 또한 표현해주어야 하는데, v[i][1] 에 노드의 번호를 담고 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
int main(){
vector<vector<int>> v;
v.resize(34);
// 각 노드의 그 다음노드 세팅, 즉 이것이 화살표 세팅이라고 보면 된다.
for(int i = 0; i <= 24; i++){
v[i].push_back(i + 1);
}
v[21][0] = 21;
v[25].push_back(31);
v[26].push_back(25);
v[27].push_back(26);
v[28].push_back(27);
v[29].push_back(30);
v[30].push_back(25);
v[31].push_back(32);
v[32].push_back(20);
v[5].push_back(22);
v[10].push_back(29);
v[15].push_back(28);
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
'algorithm > 기초' 카테고리의 다른 글
| 재귀함수를 이용한 완전탐색의 기본에 대해서 (2) (0) | 2019.12.13 |
|---|---|
| sorting algorithm(basic) (0) | 2019.03.21 |
| 재귀함수를 이용한 완전탐색의 기본에 대해서 (1) (0) | 2019.03.12 |
| BFS (1) | 2019.01.29 |


